Define: Gram-Schmidt Process

Gram–Schmidt process

From Wikipedia, the free encyclopedia

The first two steps of the Gram–Schmidt process

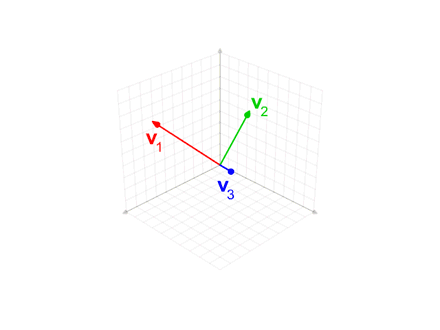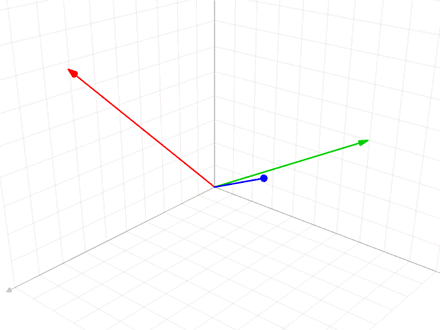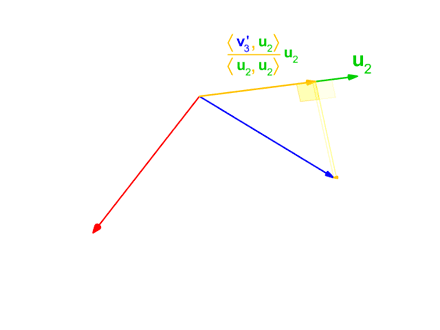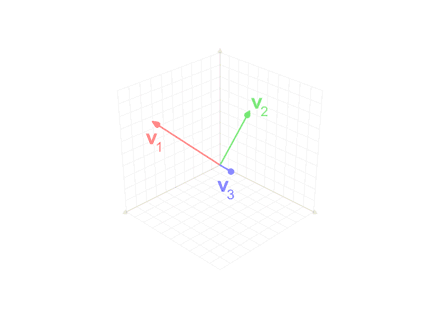
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method fororthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rⁿ equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set S = {v₁, ..., v_k} for k ≤ n and generates an orthogonal set S′ = {u₁, ..., u_k} that spans the same k-dimensional subspace of Rⁿ asS.

The method is named after Jørgen Pedersen Gram and Erhard Schmidt but it appeared earlier in the work ofLaplace and Cauchy. In the theory of Lie group decompositions it is generalized by the Iwasawa decomposition.^[1]

The application of the Gram–Schmidt process to the column vectors of a full column rank matrix yields the QR decomposition (it is decomposed into an orthogonal and a triangular matrix).

Contents

  [hide] 

• 1The Gram–Schmidt process
• 2Example
• 3Numerical stability
• 4Algorithm
• 5Determinant formula
• 6Alternatives
• 7References
• 8External links

The Gram–Schmidt process[edit]

The modified Gram-Schmidt process being executed on three linearly independent, non-orthogonal vectors of a basis for R³. Click on image for details. Modification is explained in the next section of this article.

We define the projection operator by

${\displaystyle \mathrm {proj} _{\mathbf {u} }\,(\mathbf {v} )={\langle \mathbf {v} ,\mathbf {u} \rangle \over \langle \mathbf {u} ,\mathbf {u} \rangle }\mathbf {u} ,}$

where ${\displaystyle \langle \mathbf {v} ,\mathbf {u} \rangle }$ denotes the inner product of the vectors v and u. This operator projects the vector vorthogonally onto the line spanned by vector u. If u = 0, we define ${\displaystyle \mathrm {proj} _{0}\,(\mathbf {v} ):=0}$. i.e., the projection map ${\displaystyle \mathrm {proj} _{0}}$ is the zero map, sending every vector to the zero vector.

The Gram–Schmidt process then works as follows:

${\displaystyle {\begin{aligned}\mathbf {u} _{1}&=\mathbf {v} _{1},&\mathbf {e} _{1}&={\mathbf {u} _{1} \over \|\mathbf {u} _{1}\|}\\\mathbf {u} _{2}&=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{2}),&\mathbf {e} _{2}&={\mathbf {u} _{2} \over \|\mathbf {u} _{2}\|}\\\mathbf {u} _{3}&=\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{3})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{3}),&\mathbf {e} _{3}&={\mathbf {u} _{3} \over \|\mathbf {u} _{3}\|}\\\mathbf {u} _{4}&=\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{4})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{4})-\mathrm {proj} _{\mathbf {u} _{3}}\,(\mathbf {v} _{4}),&\mathbf {e} _{4}&={\mathbf {u} _{4} \over \|\mathbf {u} _{4}\|}\\&{}\ \ \vdots &&{}\ \ \vdots \\\mathbf {u} _{k}&=\mathbf {v} _{k}-\sum _{j=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{j}}\,(\mathbf {v} _{k}),&\mathbf {e} _{k}&={\mathbf {u} _{k} \over \|\mathbf {u} _{k}\|}.\end{aligned}}}$

The sequence u₁, ..., u_k is the required system of orthogonal vectors, and the normalized vectors e₁, ..., e_k form an orthonormal set. The calculation of the sequence u₁, ...,u_k is known as Gram–Schmidt orthogonalization, while the calculation of the sequence e₁, ..., e_k is known as Gram–Schmidt orthonormalization as the vectors are normalized.

To check that these formulas yield an orthogonal sequence, first compute ‹ u₁,u₂ › by substituting the above formula for u₂: we get zero. Then use this to compute ‹ u₁,u₃ › again by substituting the formula for u₃: we get zero. The general proof proceeds by mathematical induction.

Geometrically, this method proceeds as follows: to compute u_i, it projects v_i orthogonally onto the subspace U generated by u₁, ..., u_i−1, which is the same as the subspace generated by v₁, ..., v_i−1. The vector u_i is then defined to be the difference between v_i and this projection, guaranteed to be orthogonal to all of the vectors in the subspace U.

The Gram–Schmidt process also applies to a linearly independent countably infinite sequence {v_i}_i. The result is an orthogonal (or orthonormal) sequence {u_i}_i such that for natural number n: the algebraic span of v₁, ..., v_n is the same as that of u₁, ..., u_n.

If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the 0 vector on the ith step, assuming that v_i is a linear combination of v₁, ..., v_i−1. If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.

A variant of the Gram–Schmidt process using transfinite recursion applied to a (possibly uncountably) infinite sequence of vectors ${\displaystyle (v_{\alpha })_{\alpha <\lambda }}$ yields a set of orthonormal vectors${\displaystyle (u_{\alpha })_{\alpha <\kappa }}$ with ${\displaystyle \kappa \leq \lambda }$ such that for any ${\displaystyle \alpha \leq \lambda }$, the completion of the span of ${\displaystyle \lbrace u_{\beta }:\beta <\min(\alpha ,\kappa )\rbrace }$ is the same as that of ${\displaystyle \lbrace v_{\beta }:\beta <\alpha \rbrace }$. In particular, when applied to a (algebraic) basis of a Hilbert space (or, more generally, a basis of any dense subspace), it yields a (functional-analytic) orthonormal basis. Note that in the general case often the strict inequality ${\displaystyle \kappa <\lambda }$ holds, even if the starting set was linearly independent, and the span of ${\displaystyle (u_{\alpha })_{\alpha <\kappa }}$ need not be a subspace of the span of ${\displaystyle (v_{\alpha })_{\alpha <\lambda }}$ (rather, it's a subspace of its completion).

Example[edit]

Consider the following set of vectors in R² (with the conventional inner product)

${\displaystyle S=\left\lbrace \mathbf {v} _{1}={\begin{pmatrix}3\\1\end{pmatrix}},\mathbf {v} _{2}={\begin{pmatrix}2\\2\end{pmatrix}}\right\rbrace .}$

Now, perform Gram–Schmidt, to obtain an orthogonal set of vectors:

${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1}={\begin{pmatrix}3\\1\end{pmatrix}}}$

${\displaystyle \mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{2})={\begin{pmatrix}2\\2\end{pmatrix}}-\mathrm {proj} _{({3 \atop 1})}\,({{\begin{pmatrix}2\\2\end{pmatrix}})}={\begin{pmatrix}2\\2\end{pmatrix}}-{\begin{pmatrix}4/5\end{pmatrix}}{\begin{pmatrix}3\\1\end{pmatrix}}={\begin{pmatrix}-2/5\\6/5\end{pmatrix}}.}$

We check that the vectors u₁ and u₂ are indeed orthogonal:

${\displaystyle \langle \mathbf {u} _{1},\mathbf {u} _{2}\rangle =\left\langle {\begin{pmatrix}3\\1\end{pmatrix}},{\begin{pmatrix}-2/5\\6/5\end{pmatrix}}\right\rangle =-{\frac {6}{5}}+{\frac {6}{5}}=0,}$

noting that if the dot product of two vectors is 0 then they are orthogonal.

For non-zero vectors, we can then normalize the vectors by dividing out their sizes as shown above:

${\displaystyle \mathbf {e} _{1}={1 \over {\sqrt {10}}}{\begin{pmatrix}3\\1\end{pmatrix}}}$

${\displaystyle \mathbf {e} _{2}={1 \over {\sqrt {40 \over 25}}}{\begin{pmatrix}-2/5\\6/5\end{pmatrix}}={1 \over {\sqrt {10}}}{\begin{pmatrix}-1\\3\end{pmatrix}}.}$