Texture Filtering

___
___Conceptions First
___

[Filtering Conception]

Filtering is the process of accessing a particular sample from a texture. There are two cases for filtering: minification and magnification. Magnification means that the area of the fragment in texture space is smaller than a texel, and minification means that the area of the fragment in texture space is larger than a texel. Filtering for these two cases can be set independently.
The magnification filter is controlled by the GL_TEXTURE_MAG_FILTER texture parameter. This value can be GL_LINEAR or GL_NEAREST. If GL_NEAREST is used, then the implementation will select the texel nearest the texture coordinate; this is commonly called "point sampling". If GL_LINEAR is used, the implementation will perform a weighted linear blend between the nearest adjacent samples.
The minification filter is controlled by the GL_TEXTURE_MIN_FILTER texture parameter. To understand these values better, it is important to discuss what the particular options are.

[]

___
___
___
 http://www.mbsoftworks.sk/index.php?page=tutorials&series=1&tutorial=9 (Tut source)

When telling OpenGL texture data, we must also tell it, how to FILTER the texture. What does this mean? It's the way how OpenGL takes colors from image and draws them onto a polygon. Since we will probably never map texture pixel-perfect (the polygon's on-screen pixel size is the same as texture size), we need to tell OpenGL which texels (single pixels (or colors) from texture) to take. There are several texture filterings available. They are defined for both minification and magnification. What does this mean? Well, first imagine a wall, that we are looking straight at, and its screen pixel size is the same as our texture size (256x256), so that each pixel has a corresponding texel:

www.mbsoftworks.sk

In this case, everything is OK, there is no problem. But, if we moved closer to the wall, then we need to MAGNIFY the texture - because there are now more pixels on screen than texels in texture, we must tell OpenGL how to fetch the values from texture. In this case, there are two filterings:  

NEAREST FILTERING: GPU will simply take the texel, that is nearest to exactly calculated point. This one is very fast, as no additional calculations are performed, but it's quality is also very low, since multiple pixels have the same texels, and the visual artifacts are very bold. The closer to the wall you are, the more "squary" it looks (many squares with different colors, each square represents a texel). 

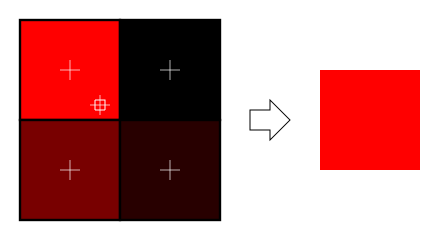GL_NEAREST

URL: Pic. Above Source

BILINEAR FILTERING: This one doesn't only get the closest texel, but rather it calculates the distances from all 4 adjacent texels, and retrieves weighted average from them, depending on the distance. This results in a lot better quality than nearest filtering, but requires a little more computational time (on modern hardware, this time is negligible). Have a look at the pictures:

www.mbsoftworks.sk

As you can see, bilinear filtering gives us smoother results. You may wonder, that I have also heard of trilinear filtering. Soon, we'll get into that as well..The second case is, if we moved further from the wall. Now the texture is bigger than the screen render of our simple wall, and thus it must be MINIFIED. The problem is, that now multiple texels may correspond to single fragment. And what shall we do now? One solution may be to average all corresponding texels, but this may be really slow, as whole texture might potentionally fall into single pixel. The nice solution to this problem is called MIPMAPPING. The original texture is stored not only in its original size, but also downsampled to all smaller resolutions, with each coordinate divided by 2, creating a "pyramid" of textures (this image is from Wikipedia):

www.mbsoftworks.sk

Particular images are called mipmaps. With mipmapping enabled, GPU selects a mipmap of appropriate size, according to the distance we see object from, and then perform some filtering. This results in higher memory consumption (exactly by 33%, as sum of 1/4, 1/16, 1/256... converges to 1/3), but gives nice visual results at very nice speed. And here is another filtering term - TRILINEAR filtering. What's that? Well, it's the almost same as bilinear filtering, but addition to it is that we take two nearest mipmaps, do the bilinear filtering on each of them, and then average results. The name TRIlinear is from the third dimension that comes into it - in case of bilinear we were finding fragments in two dimensions, trilinear filtering extends this to three dimensions.

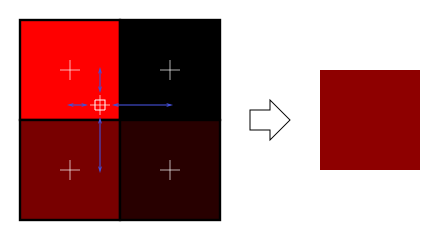GL_LINEAR

URL: Pic. Source

___
___
___