[ State ]
TO BE Continued...
[Source Tutorial Site]
http://www.3dgep.com/understanding-the-view-matrix/
[ Contents ]
...[ Column Major Matrix ]
...Convention
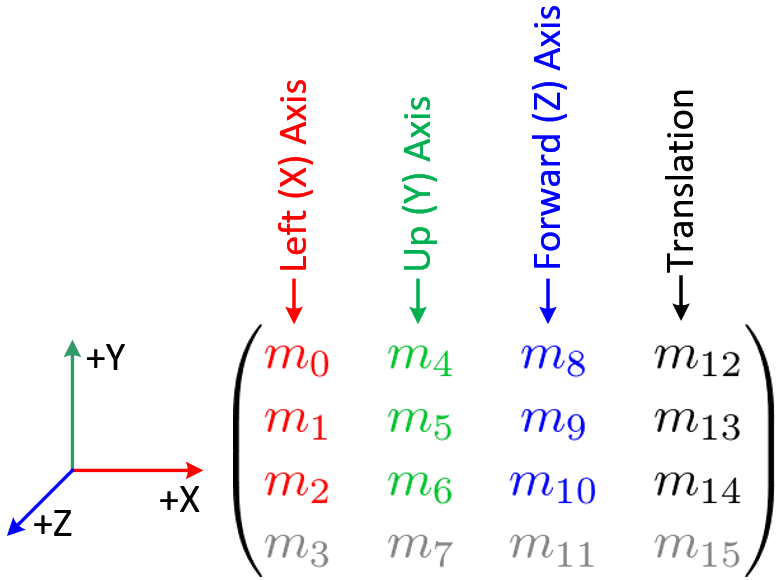
In this article I will consider matrices to be column major. That is, in a 4×4 homogeneous transformation matrix, column 1 represents the “right” (X) vector, column 2 represents the “up” (Y), column 3 represents the “forward” (Z) vector and column 4 represents the translation (origin or position) of the space represented by the transformation matrix (W).
Using this convention, we must pre-multiply column vectors to transform a vector by a transformation matrix. That is, in order to transform a vector V by a transformation matrix M we would need to pre-multiply the column vector V by the matrix M on the left.
And to concatenate a set of affine transformations (such translation (T), scale (S), and rotation R)) we must apply the transformations from left to right:
M = T * R * S
This transformation can be stated in words as “first translate, then rotate, then scale”.
And to transform a child node in a scene graph by the transform of it’s parent you would pre-multiply the child’s local (relative to it’s parent) transformation matrix by it’s parents world transform on the left:
Of course, if the node in the scene graph does not have a parent (the root node of the scene graph) then the node’s world transform is the same as its local (relative to its parent which in this case is just the identity matrix) transform:
Memory Layout of Column-Major Matrices
Using column matrices, the memory layout of the components in computer memory of a matrix are sequential in the columns of the matrix:
This has the annoying consequence that if we want to initialize the values of a matrix we must actually transpose the values in order to load the matrix correctly.
For example, the following layout is the correct way to load a column-major matrix in a C program:
1
2
3
4
5
6
7
8
9
10
11
| float right[4] = { 1, 0, 0, 0 };float up[4] = { 0, 1, 0, 0 };float forward[4] = { 0, 0, 1, 0 };float position[4] = { 0, 0, 0, 1 };float matrix[4][4] = { { right[0], right[1], right[2], right[3] }, // First col { up[0], up[1], up[2], up[3] }, // Second col { forward[0], forward[1], forward[2], forward[3] }, // Third col {position[0], position[1], position[2], position[3] } // Forth col}; |
At first glance, you will be thinking “wait a minute, that matrix is expressed in row-major format!”. Yes, this is actually true. A row-major matrix stores it’s elements in the same order in memory except the individual vectors are considered rows instead of columns.
So what is the big difference then? The difference is seen in the functions which perform matrix multiplication. Let’s see an example.
Suppose we have the following C++ definitions:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| struct vec4{ float values[4]; vec4() { values[0] = values[1] = values[2] = values[3] = 0; } vec4( float x, float y, float z, float w ) { values[0] = x; values[1] = y; values[2] = z; values[3] = w; } // Provide array-like index operators for the vector components. const float& operator[] ( int index ) const { return values[index]; } float& operator[] ( int index ) { return values[index]; }};struct mat4{ vec4 columns[4]; mat4() { columns[0] = vec4( 1, 0, 0, 0 ); columns[1] = vec4( 0, 1, 0, 0 ); columns[2] = vec4( 0, 0, 1, 0 ); columns[3] = vec4( 0, 0, 0, 1 ); } mat4( vec4 x, vec4 y, vec4 z, vec4 w ) { columns[0] = x; columns[1] = y; columns[2] = z; columns[3] = w; } // Provide array-like index operators for the columns of the matrix. const vec4& operator[]( int index ) const { return columns[index]; } vec4& operator[]( int index ) { return columns[index]; }}; |
The vec4 struct provides the index operator to allow for the use of indices to access the individual vector components. This will make the code slightly easier to read. It is interesting to note that the vec4 structure could be interpreted as either a row-vector or a column-vector. There is no way to differentiate the difference in this context.
The mat4 struct provides the index operator to allow for the use of indices to access the individual columns (not rows!) of the matrix.
1
2
3
4
5
6
| int i = row;int j = column;mat4 M;// Access the i-th row and the j-th column of matrix Mfloat m_ij = M[j][i]; |
This is quite annoying that we have to swap the i and j indices in order to access the correct matrix element. This is probably a good reason to use row-major matrices instead of column-major matrices when programming however the most common convention in linear algebra textbooks and academic research papers is to use column-major matrices. So the preference to use column-major matrices is mostly for historical reasons.
Suppose now that we define the following functions:
1
2
3
4
5
6
| // Pre-multiply a vector by a multiplying a matrix on the left.vec4 operator*( const mat4& m, const vec4& v );// Post-multiply a vector by multiplying a matrix on the right.vec4 operator*( const vec4& v, const mat4& m );// Matrix multiplicationmat4 operator*( const mat4& m1, const mat4& m2 ); |
The first method performs pre-multiplication of 4-component column vector with a 4×4 matrix. The second method performs post-multiplication of a 4-component row vector with a 4×4 matrix.
And the third method performs 4×4 matrix-matrix multiplication.
And the third method performs 4×4 matrix-matrix multiplication.
Then the pre-multiply method would look like this:
1
2
3
4
5
6
7
8
9
10
| // Pre-multiply a vector by a matrix on the left.vec4 operator*( const mat4& m, const vec4& v ){ return vec4( m[0][0] * v[0] + m[1][0] * v[1] + m[2][0] * v[2] + m[3][0] * v[3], m[0][1] * v[0] + m[1][1] * v[1] + m[2][1] * v[2] + m[3][1] * v[3], m[0][2] * v[0] + m[1][2] * v[1] + m[2][2] * v[2] + m[3][2] * v[3], m[0][3] * v[0] + m[1][3] * v[1] + m[2][3] * v[2] + m[3][3] * v[3] );} |
Notice that we still multiply the rows of matrix m with the column vector v but the indices ofm simply appear swapped.
And similarly the function which takes a 4-component row-vector v and pre-multiplies it by a 4×4 matrix m.
1
2
3
4
5
6
7
8
9
10
| // Pre-multiply a vector by a matrix on the right.vec4 operator*( const vec4& v, const mat4& m ){ return vec4( v[0] * m[0][0] + v[1] * m[0][1] + v[2] * m[0][2] + v[3] * m[0][3], v[0] * m[1][0] + v[1] * m[1][1] + v[2] * m[1][2] + v[3] * m[1][3], v[0] * m[2][0] + v[1] * m[2][1] + v[2] * m[2][2] + v[3] * m[2][3], v[0] * m[3][0] + v[1] * m[3][1] + v[2] * m[3][2] + v[3] * m[3][3] );} |
In this case we multiply the row vector v by the columns of matrix m. Notice that we still need to swap the indices to access the correct column and row of matrix m.
And the final function which performs a matrix-matrix multiply:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| // Matrix multiplicationmat4 operator*( const mat4& m1, const mat4& m2 ){ vec4 X( m1[0][0] * m2[0][0] + m1[1][0] * m2[0][1] + m1[2][0] * m2[0][2] + m1[3][0] * m2[0][3], m1[0][1] * m2[0][0] + m1[1][1] * m2[0][1] + m1[2][1] * m2[0][2] + m1[3][1] * m2[0][3], m1[0][2] * m2[0][0] + m1[1][2] * m2[0][1] + m1[2][2] * m2[0][2] + m1[3][2] * m2[0][3], m1[0][3] * m2[0][0] + m1[1][3] * m2[0][1] + m1[2][3] * m2[0][2] + m1[3][3] * m2[0][3] ); vec4 Y( m1[0][0] * m2[1][0] + m1[1][0] * m2[1][1] + m1[2][0] * m2[1][2] + m1[3][0] * m2[1][3], m1[0][1] * m2[1][0] + m1[1][1] * m2[1][1] + m1[2][1] * m2[1][2] + m1[3][1] * m2[1][3], m1[0][2] * m2[1][0] + m1[1][2] * m2[1][1] + m1[2][2] * m2[1][2] + m1[3][2] * m2[1][3], m1[0][3] * m2[1][0] + m1[1][3] * m2[1][1] + m1[2][3] * m2[1][2] + m1[3][3] * m2[1][3] ); vec4 Z( m1[0][0] * m2[2][0] + m1[1][0] * m2[2][1] + m1[2][0] * m2[2][2] + m1[3][0] * m2[2][3], m1[0][1] * m2[2][0] + m1[1][1] * m2[2][1] + m1[2][1] * m2[2][2] + m1[3][1] * m2[2][3], m1[0][2] * m2[2][0] + m1[1][2] * m2[2][1] + m1[2][2] * m2[2][2] + m1[3][2] * m2[2][3], m1[0][3] * m2[2][0] + m1[1][3] * m2[2][1] + m1[2][3] * m2[2][2] + m1[3][3] * m2[2][3] ); vec4 W( m1[0][0] * m2[3][0] + m1[1][0] * m2[3][1] + m1[2][0] * m2[3][2] + m1[3][0] * m2[3][3], m1[0][1] * m2[3][0] + m1[1][1] * m2[3][1] + m1[2][1] * m2[3][2] + m1[3][1] * m2[3][3], m1[0][2] * m2[3][0] + m1[1][2] * m2[3][1] + m1[2][2] * m2[3][2] + m1[3][2] * m2[3][3], m1[0][3] * m2[3][0] + m1[1][3] * m2[3][1] + m1[2][3] * m2[3][2] + m1[3][3] * m2[3][3] ); return mat4( X, Y, Z, W );} |
This function multiplies the rows of m1 by the columns of m2. Notice we have to swap the indices in both m1 and m2.
This function can be written slightly simplified if we reuse the pre-multiply function:
1
2
3
4
5
6
7
8
9
10
| // Matrix multiplicationmat4 operator*( const mat4& m1, const mat4& m2 ){ vec4 X = m1 * m2[0]; vec4 Y = m1 * m2[1]; vec4 Z = m1 * m2[2]; vec4 W = m1 * m2[3]; return mat4( X, Y, Z, W );} |
The main point is that whatever convention you use, you stick with it and be consistent and always make sure you document clearly in your API which convention you are using.
...



No comments:
Post a Comment