[ Concept ]
changes are illusion caused by matrix transformation
neither the camera nor the world moves, which is of non-existence
[ The Model Matrix ]
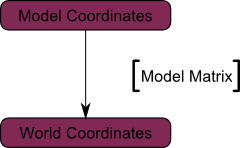
...This model, just as our beloved red triangle, is defined by a set of vertices. The X,Y,Z coordinates of these vertices are defined relative to the object’s center : that is, if a vertex is at (0,0,0), it is at the center of the object.
 |
| Object Space |
We’d like to be able to move this model, maybe because the player controls it with the keyboard and the mouse. Easy, you just learnt do do so :translation*rotation*scale, and done. You apply this matrix to all your vertices at each frame (in GLSL, not in C++!) and everything moves. Something that doesn’t move will be at the center of the world.
 |
| World Space |
Your vertices are now in World Space. This is the meaning of the black arrow in the image below : We went from Model Space (all vertices defined relatively to the center of the model) to World Space (all vertices defined relatively to the center of the world).
 |
| Transformation |
...
[ The View Matrix ]
...
So initially your camera is at the origin of the World Space. In order to move the world, you simply introduce another matrix. Let’s say you want to move your camera of 3 units to the right (+X). This is equivalent to moving your whole world (meshes included) 3 units to the LEFT ! (-X). While you brain melts, let’s do it :
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);
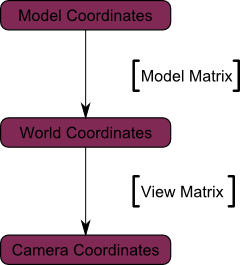
Again, the image below illustrates this : We went from World Space (all vertices defined relatively to the center of the world, as we made so in the previous section) to Camera Space (all vertices defined relatively to the camera).
 |
| World-Space TO Camera-Space |
Before you head explodes from this, enjoy GLM’s great glm::lookAt function:
glm::mat4 CameraMatrix = glm::lookAt(
cameraPosition, // the position of your camera, in world space
cameraTarget, // where you want to look at, in world space
upVector // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);
Here’s the compulsory diagram :
...
[ The Projection Matrix ]
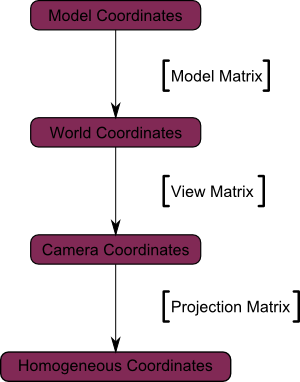
...We’re now in Camera Space. This means that after all theses transformations, a vertex that happens to have x==0 and y==0 should be rendered at the center of the screen. But we can’t use only the x and y coordinates to determine where an object should be put on the screen : its distance to the camera (z) counts, too ! For two vertices with similar x and y coordinates, the vertex with the biggest z coordinate will be more on the center of the screen than the other.
This is called a perspective projection :
 |
| Projection Matrix |
And luckily for us, a 4x4 matrix can represent this projection1 :
// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless// FoV //- The horizontal Field of View, in degrees : the amount of "zoom". // - Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
// 4.0f/3.0f//- Aspect Ratio. Depends on the size of your window. // - Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?
// 0.1f//- Near clipping plane. Keep as big as possible, or you'll get precision issues.
// 100.0f//- Far clipping plane. Keep as little as possible.
glm::mat4 projectionMatrix = glm::perspective(FoV,4.0f / 3.0f,0.1f,100.0f);
The near and far arguments may seem unnecessary, but they are used to define the possible range of depths for the Z-buffer. Therefore, too large a range will result in Z-buffer precision problems.
One last time :
We went from Camera Space (all vertices defined relatively to the camera) to Homogeneous Space (all vertices defined in a small cube. Everything inside the cube is onscreen).And the final diagram :
...
[]
...
*****************************************************************************
*
* IMPORTANT CLUE
*
*****************************************************************************
Understanding Mathematically
Projection View moves around space and change its orientation. The first thing to notice is that the desired projection on the screen does not change with view direction.
For this reason, we transform other things to get the desired projection.
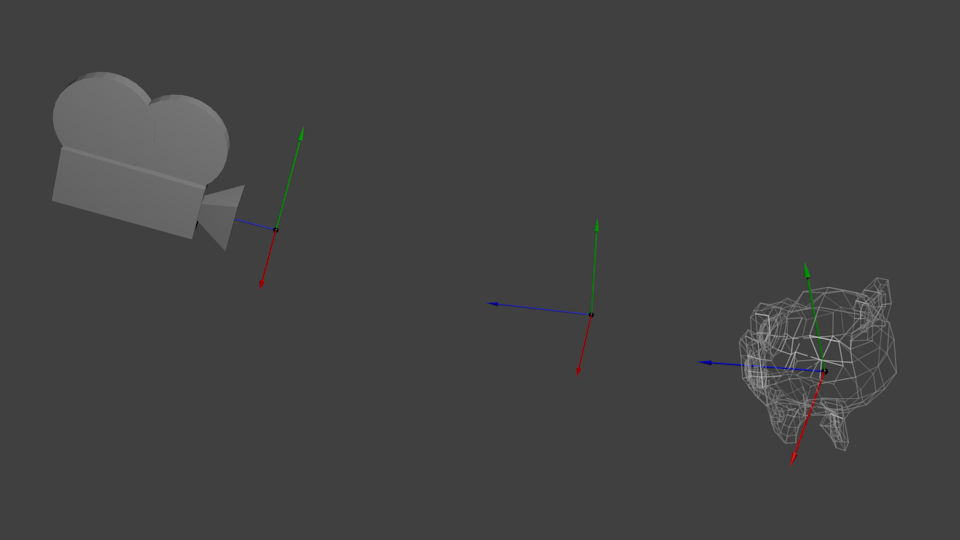
No comments:
Post a Comment